Algorytm Euklidesa służy do wyznaczania największego wspólnego dzielnika dwóch liczb całkowitych. Największy wspólny dzielnik dwóch liczb a i b, to taka liczba, która dzieli te liczby bez reszty i jest ona możliwie największa. Można go zastosować do skracania ułamków lub wyznaczenia najmniejszej wspólnej wielokrotności NWW.
Artykuł opisuje dwie postacie algorytmu: nieoptymalną i optymalną.
Niezoptymalizowany algorytm Euklidesa
Sposób rozwiązania jest następujący.
Wybieramy większą z dwóch liczb i zamieniamy ją na różnicę większej i mniejszej. Czynność tą powtarzamy do momentu uzyskania dwóch takich samych wartości.
Prześledźmy przykład dla liczb 12 i 18. Wiadomo, że NWD(12,18)=6

Dla liczb 28 i 24NWD(28,24)=4:NWD(28,24)=4:
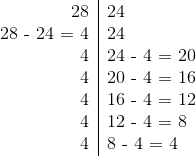
Warto zaznaczyć, że ten algorytm jest bardzo niewydajny. Gdy dobierzemy odpowiednio liczby, to ilość operacji znacznie się zwiększy. Przeanalizujmy takie liczby jak 1 i 10000:

W tym przypadku najmniejszy wspólny dzielnik jest równy jeden. Żeby to stwierdzić, należy wykonać 9999 kroków przejść pętli. Dla większych liczb algorytm może nie sprostać zadaniu.
Algorytm można testować na automatycznej sprawdzarce
Rozwiązanie iteracyjne:
//algorytm.edu.pl
#include<iostream>
using namespace std;
int NWD(int a, int b)
{
while(a!=b)
if(a>b)
a-=b; //lub a = a - b;
else
b-=a; //lub b = b-a
return a; // lub b - obie zmienne przechowują wynik NWD(a,b)
}
int main()
{
int a, b;
cout<<"Podaj dwie liczby: ";
cin>>a>>b;
cout<<"NWD("<<a<<","<<b<<") = "<<NWD(a,b)<<endl;
return 0;
}
Rozwiązanie rekurencyjnie:
//algorytm.edu.pl
#include<iostream>
using namespace std;
int NWD(int a, int b)
{
if(a!=b)
return NWD(a>b?a-b:a,b>a?b-a:b);
return a;
}
int main()
{
int a, b;
cout<<"Podaj dwie liczby: ";
cin>>a>>b;
cout<<"NWD("<<a<<","<<b<<") = "<<NWD(a,b)<<endl;
system("pause");
return 0;
}
Zakładamy, że liczbya>0,b>0.a>0,b>0.
Uwaga!NWD(a,0)=a,NWD(a,0)=a,gdzie a > 0,NWD(0,b)=b,NWD(0,b)=b,gdzie b > 0. Ten przypadek nie jest rozpatrzony w algorytmie.
Zoptymalizowany algorytm Euklidesa
W przypadku optymalnego rozwiązania NWD postępujemy następująco:
załóżmy, że wyznaczamy NWD dwóch liczb naturalnych a i b. W każdym przejściu pętli wykonujemy dwie operacje
a=ba=b
b=a mod bb=a mod b
Czynności te powtarzamy do momentu, gdy zmienna b osiągnie wartość zero. Zmienna a będzie przechowywać wtedy największy wspólny dzielnik liczb podanych na wejściu. Przeanalizujmy przykłady:
PoliczmyNWD(12,18)=6NWD(12,18)=6:
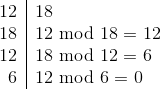
Dla liczb 28 i 24:
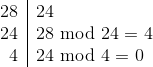
Natomiast dla liczb 10000 i 1:
![]()
Rozwiązanie iteracyjne w C++:
//algorytm.edu.pl
#include<iostream>
using namespace std;
int NWD(int a, int b)
{
int pom;
while(b!=0)
{
pom = b;
b = a%b;
a = pom;
}
return a;
}
int main()
{
int a, b;
cout<<"Podaj dwie liczby: ";
cin>>a>>b;
cout<<"NWD("<<a<<","<<b<<") = "<<NWD(a,b)<<endl;
return 0;
}Rozwiązanie rekurencyjne:
//algorytm.edu.pl
#include<iostream>
using namespace std;
int NWD(int a, int b)
{
if(b!=0)
return NWD(b,a%b);
return a;
}
int main()
{
int a, b;
cout<<"Podaj dwie liczby: ";
cin>>a>>b;
cout<<"NWD("<<a<<","<<b<<") = "<<NWD(a,b)<<endl;
return 0;
}Warto zauważyć, że algorytm poprawnie wyznacza NWD w przypadku, gdy jedna z liczb jest równa zero.